9급 국가직 공무원 수학 필기 기출문제(해설) 및 CBT 모의고사(2025년 11월 24일)(2291203)
최강 자격증 기출문제 전자문제집 CBT : www.comcbt.com
전자문제집 CBT란?
종이 문제집이 아닌 인터넷으로 문제를 풀고 자동으로 채점하며 모의고사, 오답 노트, 해설까지 제공하는
무료 기출문제 학습 프로그램으로 실제 상설검정에서 사용하는 OMR 형식의 CBT를 제공합니다.
최신 9급 국가직 공무원 수학 필기 기출문제 : [다운로드]
| 10. | 첫째항이 1/3, 공비가 r(r≠0)인 등비수열 {an}의 첫째항부터 n제항까지의 합을 Sn이라 할 때, S4 - S2 = a22이다. S4 = q/p일 때, q의 값은? (단, p, q는 서로소인 자연수)(2021년 04월) |
정답 : [1 ]
정답률 : 16%
| | <문제 해설>
a_1 = 1/3
a_2 = 1/3 * r
a_3 = 1/3 * r^2
a_4 = 1/3 * r^3
S_1 = a_1
S_2 = a_1 + a_2
S_3 = a_1 + a_2 + a_3
S_4 = a_1 + a_2 + a_3 + a_4
이므로,
S_1 = 1/3
S_2 = 1/3 * (1 + r)
S_3 = 1/3 * (1 + r + r^2)
S_4 = 1/3 * (1 + r + r^2 + r^3)
=> S_4 - S_2 = 1/3 * (1 + r + r^2 + r^3) - 1/3 * (1 + r) , (a_2)^2 = (1/3 * r)^2 = 1/9 * r^2
= 1/3 * (r^2 + r^3)
이므로,
1/3 * (r^2 + r^3) = 1/9 * r^2
=> 3 * (r^2 + r^3) = r^2
=> 3r^3 + 2r^2 = 0
=> r^2(3r + 2) = 0
이때, r이 0이 아니므로, r = -2/3
그러므로,
S_4 = S_2 + (a_2)^2
= (1/3 * (1 + r)) + (1/9 * r^2)
= (1/3 * 1/3) + (1/9 * 4/9)
= 1/9 + 4/81
= 13/81
그러므로,
13/81 = q/p
=> q = 13
[해설작성자 : 찍먹] |
|
정 답 지9급 국가직 공무원 수학 필기 기출문제(해설) 및 CBT 모의고사(2025년 11월 24일)(2291203)
최강 자격증 기출문제 전자문제집 CBT : www.comcbt.com
전자문제집 CBT란?
종이 문제집이 아닌 인터넷으로 문제를 풀고 자동으로 채점하며 모의고사, 오답 노트, 해설까지 제공하는
무료 기출문제 학습 프로그램으로 실제 상설검정에서 사용하는 OMR 형식의 CBT를 제공합니다.
최신 9급 국가직 공무원 수학 필기 기출문제 : [다운로드]
| 10. | 첫째항이 1/3, 공비가 r(r≠0)인 등비수열 {an}의 첫째항부터 n제항까지의 합을 Sn이라 할 때, S4 - S2 = a22이다. S4 = q/p일 때, q의 값은? (단, p, q는 서로소인 자연수)(2021년 04월) |
정답 : [1 ]
정답률 : 16%
| | <문제 해설>
a_1 = 1/3
a_2 = 1/3 * r
a_3 = 1/3 * r^2
a_4 = 1/3 * r^3
S_1 = a_1
S_2 = a_1 + a_2
S_3 = a_1 + a_2 + a_3
S_4 = a_1 + a_2 + a_3 + a_4
이므로,
S_1 = 1/3
S_2 = 1/3 * (1 + r)
S_3 = 1/3 * (1 + r + r^2)
S_4 = 1/3 * (1 + r + r^2 + r^3)
=> S_4 - S_2 = 1/3 * (1 + r + r^2 + r^3) - 1/3 * (1 + r) , (a_2)^2 = (1/3 * r)^2 = 1/9 * r^2
= 1/3 * (r^2 + r^3)
이므로,
1/3 * (r^2 + r^3) = 1/9 * r^2
=> 3 * (r^2 + r^3) = r^2
=> 3r^3 + 2r^2 = 0
=> r^2(3r + 2) = 0
이때, r이 0이 아니므로, r = -2/3
그러므로,
S_4 = S_2 + (a_2)^2
= (1/3 * (1 + r)) + (1/9 * r^2)
= (1/3 * 1/3) + (1/9 * 4/9)
= 1/9 + 4/81
= 13/81
그러므로,
13/81 = q/p
=> q = 13
[해설작성자 : 찍먹] |
|
정 답 지
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
② | ③ | ④ | ③ | ④ | ③ | ① | ① | ④ | ① |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ③ | ③ | ③ | ④ | ④ | ① | ① | ④ | ① | ① |
9급 국가직 공무원 수학 필기 기출문제(해설) 및 CBT 모의고사(2025년 11월 24일)(2291203)을 이용해 주셔서 감사합니다.
, 필기, 기출문제, 전자문제집, CBT, 온라인, 모의테스트, 모의고사

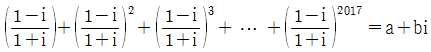 일 때, a+b 의 값은? (단, a, b 는 실수)(2017년 04월)
일 때, a+b 의 값은? (단, a, b 는 실수)(2017년 04월)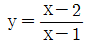
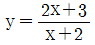
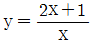
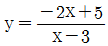
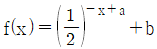 의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?(2021년 04월)
의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?(2021년 04월)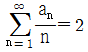 일 때,
일 때, 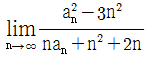 의 값은?(2014년 04월)
의 값은?(2014년 04월)
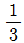
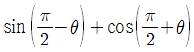 의 값은?(2014년 04월)
의 값은?(2014년 04월)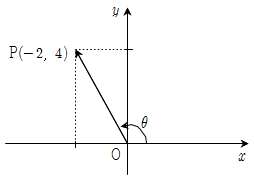
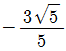
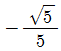
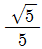
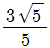
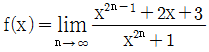 에 대하여
에 대하여 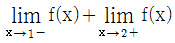 의 값은?(2017년 04월)
의 값은?(2017년 04월)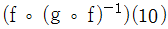 의 값은?(2018년 04월)
의 값은?(2018년 04월)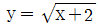 의 그래프를 y축에 대하여 대칭이동한 후, 다시 x축 양의 방향으로 1만큼 평행이동한 그래프가 점 (a, 3)을 지날 때, a의 값은?(2014년 04월)
의 그래프를 y축에 대하여 대칭이동한 후, 다시 x축 양의 방향으로 1만큼 평행이동한 그래프가 점 (a, 3)을 지날 때, a의 값은?(2014년 04월)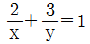 일 때, x+y의 최솟값은?(2019년 04월)
일 때, x+y의 최솟값은?(2019년 04월)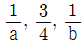 도 이 순서대로 등차수열을 이룰 때,
도 이 순서대로 등차수열을 이룰 때,  의 값은?(2018년 04월)
의 값은?(2018년 04월)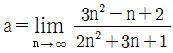 이고
이고 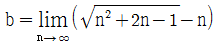 일 때, a+b 의 값은?(2017년 04월)
일 때, a+b 의 값은?(2017년 04월)