2020년08월22일 기출문제
| 61. |
좌표계의 원점이 중심이고 경도 u, 위도 v로 표시되는 구의 매개 변수식
경도 좌표는 세로줄로, 경도가 0에서 증가하면 x축 (+) 방향에서 y축 (+) 방향으로 반시계 방향으로 돈다. 위도 좌표는 가로줄로, 위도가 0에서 증가하면 x-y평면 (+)에서 z축 (+) 방향으로 반시계 방향으로 돈다. 위도를 2개로 나눠보면, z축에 해당하는 Rsin(v). x-y평면에 해당하는 Rcos(v)로 나눌 수 있고
Rcos(v)에서 경도를 2개로 나눠보면 x축에 해당하는 Rcos(v)cos(u), y축에 해당하는 Rcos(v)sin(u)로 나눌 수 있다.
각각의 축에 해당하는 단위벡터를 붙여 하나의 식으로 표현하면,
Rcos(v)cos(u)i+Rcos(v)sin(u)j+Rsin(v)k가 된다.
|
으로 옳은 것은? (단, 구의 반경은 R로 가정하고, 
는 각각 x, y, z축 방향의 단위벡터이며, 0≦u≦2π, 
이다.)
그림풀이
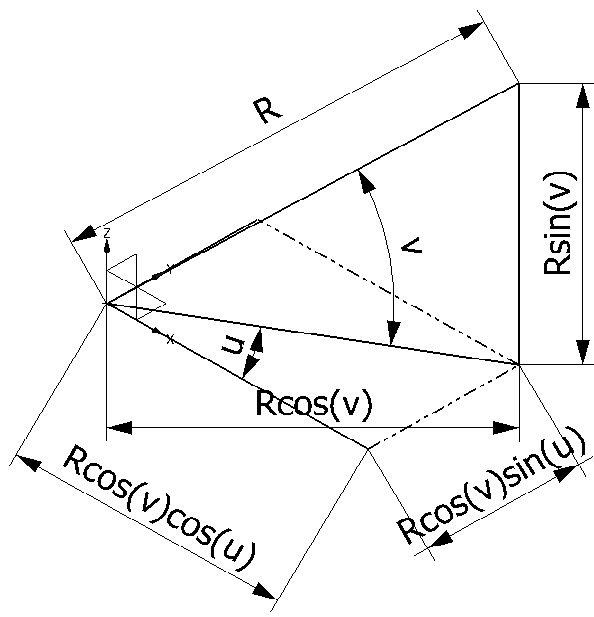
이글 보시면 자격증명 적어 주시면 감사하겠습니다.